Question

(a) Find the domain off (x) = ln(ex − 3).
(b) Find F −1 and its domain.

Answer 1

a) The domain of f(x) is
`x > 1.1`.

b)

The inverse function is:

So we need

`e^(x) - 3 > 0`

`e^(x) > 3`

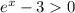
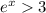
Applying ln to both sides

`\ln{e^(x)} > ln(3)`

`x > 1.1`

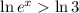
So the domain of f(x) is
`x > 1.1`.

(b) Find F −1 and its domain.

`F^(-1)` is the inverse function of f.

How do we find the inverse function?

To find the inverse equation, we change y with x to form the new equation, and then we isolate y in the new equation. So:

Original equation:

f(x) = y = \ln{e^{x} - 3}

New equation

`x = \ln{e^(y) - 3}`

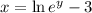
Here, we apply the exponential to both sides:

`e^(x) = e^{\ln{e^(y) - 3}}`

`e^(y) - 3 = e^(x)`

`e^(y) = e^(x) + 3`

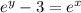
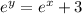
Applying ln to both sides

`\ln{e^(y)} = \ln{e^(x) + 3}`

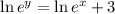
The inverse function is:

`y = \ln{e^(x) + 3}`

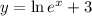
The domain is

`e^(x) + 3 > 0`

`e^(x) > -3`

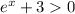
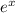`e^(x)` is always a positive number, so it is always going to be larger than -3 no matter the value of x. So the domain are all the real values.