Question

How many five card hands consisting of 2 kings and 3 aces can be dealt from a deck of 52 playing cards?

Answer 1

24.

Explanation:

In a standard deck of 52 cards, there are four kings and four aces.

Permutation
`\displaystyle {n \choose k}` gives the number of ways to choose
`k` items out of a pile of
`n` of these items. The equation for calculating

`\displaystyle {n \choose k} = (n!)/((n - k)! \cdot k!)`.

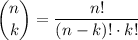Consider: how many ways to choose two kings out of four? Assume that the order for choosing the two cards does not matter. The number of possible ways can be found using the following permutation:

`\displaystyle {4 \choose 2} = (4!)/((4 - 2)! \cdot 2!) = (4!)/(2! \cdot 2!)=(4 * 3 * 2 * 1)/((2 * 1) * (2 * 1)) = 6`.

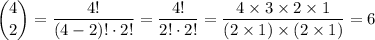Similarly, find the number of ways to choose three aces out of four.

`\displaystyle {4 \choose 3} = (4!)/((4 - 3)! \cdot 3!) = (4!)/(1! \cdot 3!)(4 * 3)/(1 * (3 * 2 * 1)) = 4`.

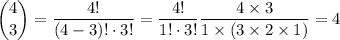Note that

• No card other than the two kings and the three aces are involved in this choice of five cards.
• The choice of the two kings is independent of the choice the choice of the aces. (Choosing some kings does not change the choices of aces, and vice versa for the choice of the kings.)

Therefore, multiply these two permutations to find the number of ways to choose these five cards:

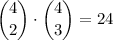`\displaystyle {4 \choose 2} \cdot {4 \choose 3}= 24`.