Final answer:
To find the derivative f'(x) of the function
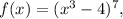 one must apply the chain rule. The chain rule gives us
one must apply the chain rule. The chain rule gives us
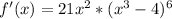 as the solution.
as the solution.
Step-by-step explanation:
The question is asking to find the derivative of the function
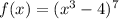 . To solve this, we use the chain rule for differentiation, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function multiplied by the derivative of the inner function. In this case, the outer function is
. To solve this, we use the chain rule for differentiation, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function multiplied by the derivative of the inner function. In this case, the outer function is
 and the inner function is
and the inner function is
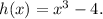
The derivative of
 with respect to u is
with respect to u is
 . The derivative of h
. The derivative of h
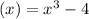 with respect to x is
with respect to x is
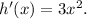 Applying the chain rule, we get:
Applying the chain rule, we get:
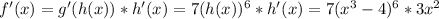
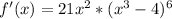 is the derivative of the function f(x).
is the derivative of the function f(x).