Answer:
924.376 Hz
Step-by-step explanation:
Data provided in the question:
Velocity of the ambulance, v = 99.9 km/h =
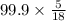 m/s
m/s
= 27.75 m/s
Frequency of the sound, f₀ = 786 Hz
Speed of the sound, V = 343 m/s
Now,
Using the Doppler's effect formula, we have
Frequency heard =
![f_0*[(V+v)/(V-v)]](https://img.qammunity.org/2021/formulas/physics/college/n82dfxy8vyvgk9co4n6by0vy5kve9r22a5.png)
Thus,
Frequency heard =
![786*[(343+27.75)/(343-27.75)]](https://img.qammunity.org/2021/formulas/physics/college/13wvrspwz3gjhimfdv7i090bacxtghqdny.png)
or
Frequency heard = 786 × 1.176
or
Frequency heard = 924.376 Hz