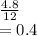Question

A point is randomly selected from within a triangle with vertices at (0, 0), (0, 4) and (6, 0). What is the probability that the x-coordinate of the selected point is less than the y-coordinate? The probability will be the fraction of the total area which this is true, so you'll also need your triangle area formula.

Answer 1

0.4

Explanation:

Given that a point is randomly selected from within a triangle with vertices at (0, 0), (0, 4) and (6, 0).

To find the probability that the x-coordinate of the selected point is less than the y-coordinate

The favourable region would be the region formed by the given line, y axis, and the line x=y

For the region area = area of triangle with vertices (0,0) (0,4) and (2.4,2.4)

Base of triangle = 4 and height =2.4

Area = 1/2 (4) (2.4) = 4.8

Area of full triangle given has base as 6 and height as 4

Area = 1/2 (6)(4) = 12

So probability=
`(4.8)/(12) \\=0.4`