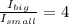Question

Two uniform solid spheres have the same mass, but one has twice the radius of the other. The ratio of the larger sphere's moment of inertia about a central axis to that of the smaller sphere is

Answer 1

The ratio is 4

Step-by-step explanation:

The moment of inertia of a solid sphere about a central axis is:

`I=(2mr^(2))/(5)`

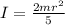
With m the mass and r the radius of the sphere.

For the smaller sphere with mass M and radius R the moment of inertia is:

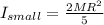`I_(small) =(2MR^(2))/(5)` (1)

For the bigger sphere with mass M and radius 2R the moment of inertia is:

`I_(big)=(2M(2R)^(2))/(5)`

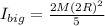
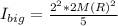`I_(big)=(2^(2)*2M(R)^(2))/(5)` (2)

The ratio between larger of the larger sphere's moment of inertia about a central axis to that of the smaller sphere is the ratio between (2) and (1):

`(I_(big))/(I_(small))=((4*2M(R)^(2))/(5))/((2M(R)^(2))/(5))`

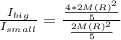
The term
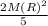`(2M(R)^(2))/(5)` cancels, so:

`(I_(big))/(I_(small))=4`