Question

Find the present value of $325 due in the future under each of the following conditions. Do not round intermediate calculations. Round your answers to the nearest cent.

(a) 9% nominal rate, semiannual compounding, discounted back 5 years.
(b) 9% nominal rate, quarterly compounding, discounted back 5 years.
(c) 9% nominal rate, monthly compounding, discounted back 1 year.

Answer 1

a. $209.28

b. $134.76

c. $191.64

Step-by-step explanation:

The present value with compound interest equation is the following.

PV =
`(A)/((1 + r/n)^nt)`

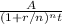
Where,

A = Final amount.

PV = Present value

r = interest rate in decimal.

n = number of times the interest is compounded every year.

t = number of years of investment

a. PV =
`(A)/((1 + r/n)^nt)`

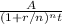
A = 325

r = 9% = 0.09

n = 2

t = 5

PV = 325/(1+0.09/2)^2x5

= 325/(1+0.045)^10

= 325/(1.045)^10

= 325/1.552969422

= 209.2764966

= $209.28

That is, the present value of $325 at 9% nominal rate, semiannual compounding, discounted back 5 year is $209.28

b. PV =
`(A)/((1 + r/n)^nt)`

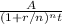
A = 325

r = 9% = 0.09

n = 4

t = 5

PV = 325/(1+0.09/2)^4x5

= 325/(1+0.045)^20

= 325/(1.045)^20

= 325/2.411714025

= 134.7589294

= $134.76

That is, the present value of $325 at 9% nominal rate, quarterly compounding, discounted back 5 year is $134.76

c. PV =
`(A)/((1 + r/n)^nt)`

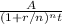
A = 325

r = 9% = 0.09

n = 12

t = 1

PV = 325/(1+0.09/2)^12x1

= 325/(1+0.045)^12

= 325/(1.045)^12

= 325/1.695881433

= 191.6407561

= $191.64

That is, the present value of $325 at 9% nominal rate, monthly compounding, discounted back 1 year is $191.64

Answer 2

(a) PV = $209.28

(b) PV = $208.33

(c) PV = $207.58

Step-by-step explanation:

DF = (1 + (i/n) )-n*t

(a) PV= $325 ( 1+(0.09/2) )^-5(2)

PV= $325 x 0.644

PV= $209.28

(b) PV= $325 ( 1+(0.09/4) )^-5(4)

PV =$325 x 0.641

PV =$208.33

(c) PV= $325 (1+(0.09/12) )^-5(12)

PV= $325 x 0.639

PV=$207.58