Question

At a certain instant a ball passes location < 8, 18, -15 > m. In the next 3 seconds, the ball's average velocity is < -11, 30, 23 > m/s. At the end of this 3 second time interval, what is the height y of the ball?

Answer 1

108 m

Step-by-step explanation:

We can calculate the new position of the ball by adding the initial position to the change in position, which equals to product of average velocity (v = < -11, 30, 23 > m/s) and time (t = 3s)

`s = s_0 + \Delta s = s_0 + vt = <8, 18, -15> + 3<-11, 30, 23>`

`s = <8, 18, -15> + <-33, 90, 69>`

`s = <-25, 108, 54>`

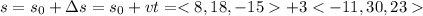
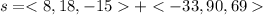
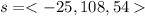
So the new height y of the ball at the end of 3s time is 108m