Question

Two number cubes are rolled sequentially. What is the probability that the first number cube shows a five and the other number cube shows an even number?

Answer 1

1/12

e

e

e

e

e

e

e

e

e

e

Answer 2

The probability of first number cube shows a five and the other number cube shows an even number is
`(1)/(12)`.

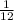Solution:

Two cubes are rolled sequentially.

Sample space when two dies are rolled

`=\left\{\begin{array}{l}{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)} \\{(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)} \\{(3,1), 3(, 2),(3,3),(3,4),(3,5),(3,6)} \\{(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)} \\{(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)} \\{(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}\end{array}\right\}`

Number of sample space = 36

Even numbers getting when two cubes rolled are 2, 4, 6.

First number cube shows a five and the other number cube shows an even number = {(5, 2), (5, 4), (5 6)}

Number of first number cube shows a five and the other number cube shows an even number = 3

Probability of first number cube shows a five and the other number cube shows an even number

`$=\frac{\text{Number of outcomes}}{\text{Total number of sample space}} $`

`$=(3)/(36)`

`$=(1)/(12)`

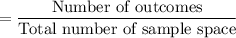
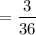
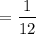
Hence, the probability of first number cube shows a five and the other number cube shows an even number is
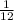`(1)/(12)`.