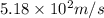Question

A volume of nitrogen gas has a density of 1.301.30 kg/m3 and a pressure of 1.151.15 atm. Find the temperature of the gas and the rms speed of its molecules.

Answer 1

The temperature of the gas is, 301.7 K

The root mean square speed is,
`5.18* 10^(2)m/s`

Explanation :

To calculate the volume of argon gas we are using ideal gas equation:

`PV=nRT\\\\PV=(w)/(M)RT\\\\P=(w)/(V)* (RT)/(M)\\\\P=(\rho RT)/(M)`

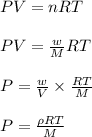
where,

P = pressure of nitrogen gas = 1.15 atm

V = volume of nitrogen gas

T = temperature of nitrogen gas

R = gas constant = 0.0821 L.atm/mole.K

w = mass of nitrogen gas

M = molar mass of nitrogen gas = 28 g/mole

`\rho` = density of nitrogen gas =
`1.30kg/m^3=1.30g/L`

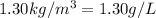
Now put all the given values in the ideal gas equation, we get:

`1.15atm=((1.30g/L)* (0.0821L.atm/mole.K)* T)/(28g/mol)`

`T=301.7K`

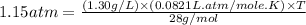
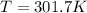
Therefore, the temperature of the gas is, 301.7 K

Now we have to determine the root mean square speed of the molecule.

The formula used for root mean square speed is:

`\\u_(rms)=\sqrt{(3kN_AT)/(M)}`

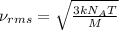
where,

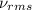`\\u_(rms)` = root mean square speed

k = Boltzmann’s constant =
`1.38* 10^(-23)J/K`

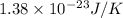
T = temperature = 301.7 K

M = atomic mass of nitrogen gas = 0.028 kg/mole

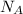`N_A` = Avogadro’s number =
`6.02* 10^(23)mol^(-1)`

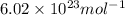
Now put all the given values in the above root mean square speed formula, we get:

`\\u_(rms)=\sqrt{(3* (1.38* 10^(-23)J/K)* (6.02* 10^(23)mol^(-1))* (301.7K))/(0.028kg/mol)}`

`\\u_(rms)=5.18* 10^(2)m/s`

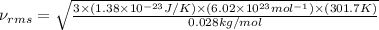
The root mean square speed is,
`5.18* 10^(2)m/s`