Question

An ice cube with a volume of 45.0ml and a density of 0.9000g/cm3 floats in a liquid with a density of 1.36g/ml. what volume of the cube is submerged in the liquid

Answer 1

Answer : The volume of the cube submerged in the liquid is, 29.8 mL

Explanation :

First we have to determine the mass of ice.

Formula used :

`\text{Mass of ice}=\text{Density of ice}* \text{Volume of ice}`

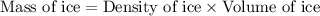
Given:

Density of ice =
`0.9000g/cm^3=0.9000g/mL`

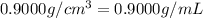
Volume of ice = 45.0 mL

`\text{Mass of ice}=0.9000g/mL* 45.0mL`

`\text{Mass of ice}=40.5g`

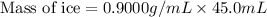
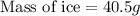
The cube will float when 40.5 g of liquid is displaced.

Now we have to determine the volume of the cube is submerged in the liquid.

`\text{Volume of ice}=\frac{\text{Mass of liquid}}{\text{Density of liquid}}`

`\text{Volume of ice}=(40.5g)/(1.36g/mL)`

`\text{Volume of ice}=29.8mL`

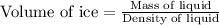
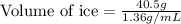
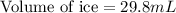
Thus, the volume of the cube submerged in the liquid is, 29.8 mL