The average speed for the entire trip from home to the gift store and back is 15 miles per hour
Solution:
Given that, Starting at home Michael travel uphill to the gift store for 24 minutes after 10 mph
1 hour = 60 minutes
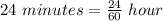
You can travel back home along the same path down hill at a speed of 30 mph
The distance is given as:
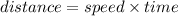
Uphill distance:
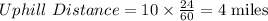
The downhill distance will also be same 4 miles at a speed of 30 mph
Find the time taken for down trip
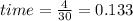
Thus, time taken for downtrip = 0.133 hours
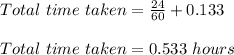
Total distance traveled = 4 miles + 4 miles = 8 miles
The average speed is given by formula:
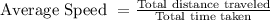
Substituting the values we get,

Thus average speed for the entire trip from home to the gift store and back is 15 miles per hour