Question

A rubber ball is dropped from a height of 12 meters. Each bounce the ball goes back up 2/3 of its previous height. How many times will the ball bounce at least 12 cm high?

Answer 1

Explanation:

This is an exponential function for which we have to find the model for this particular situation. We can make a couple of coordinates with the given info. x is the # of bounces and y is the height in meters.

We are told that before the ball bounces, its height is 12 m. In coordinate form that is (0, 12). Then after the first bounce, the ball comes back up to 2/3 its original height. 2/3 of 12 = 8, so the coordinate is (1, 8). We can now use that info to find the model function in the form

`y=a(b)^x` where y is the height of the ball, after x bounces, a is the initial value, and b is the growth or decay rate. Using the first coordinate,

`12=a(b)^0`

Since anything raised to 0 power is 1, we get that

a = 12

Now we will use the second set of coordinates to solve for b, subbing in that value for a:

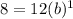`8=12(b)^1` which gives us that

b = 8/12 or 2/3

Keep in mind, that if you are well-versed in this concept, you would have been able to come up with the model from the info given without having to do the math to find it, but I figured as a teacher, I wouldn't let a teaching moment get wasted!

So the function for this situation is

`y=12((2)/(3))^x`

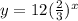
We now want to find out how many bounces, x, it will take the ball til it's at a height of 12 cm. We have our function in terms of meters, so we have to convert the cm to meters. 12 cm is .12 meters. Plug in .12 for y and solve for x:

`.12=12((2)/(3))^x`

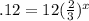
Begin by dividing both sides by 12 to get

`.01=(2)/(3)^x`

The only way to get that x out of its current position is to take the natural log of both sides:

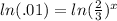`ln(.01)=ln((2)/(3))^x` and by the power rule of logs, we can pull the x down in front, giving us

`ln(.01)=xln((2)/(3))`

Divide both sides by ln(2/3) to get

`(ln(.01))/(ln((2)/(3)) )=x`

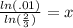
Do those calculations on your calculator to get

`(-4.605170186)/(-.4054651081)=x`

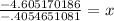
and divide that to get that

x = 11.357 or approximately 11 bounces.