Question

Do as physics instructor fred cauthen does and place a tennis ball close to and above the top of a basketball. drop the balls together. if their vertical alignment nicely remains as they fall to the floor, you'll see that the tennis ball bounces unusually high. can you reconcile this with energy conservation?

Answer 1

after shock

creating a system for the conservation of the energy of the basketball ball and creating a system for the tennis ball only, the conservation of energy should be applied to each system independently

Step-by-step explanation:

When the two balls fall they acquire the same speed since they are accelerated by the same force, their weight and the acceleration of the acceleration of gravity. When reaching the floor the mechanical energy of the system is conserved.

Upon reaching the floor, the first ball (basketball) collides with the floor, this process is very fast, at the end of the process the basketball comes out with a velicad up and collides with the much lighter tennis ball that is still descending .

we assume that the shocks are elastic, when solving the momentary and kinetic energy findings, we find the velocities after each shock

In this clash the tennis ball acquires a high kinetic speed with an upward direction that makes a very high height high. Again this shock is very fast and the tennis ball almost does not move.

Here we must separate the system, creating a system for the conservation of the energy of the basketball ball and another system for the tennis ball only, the conservation of energy should be applied to each system independently

Em₀ =K = 1/2 m v²

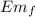`Em_(f)` = U = m g h

As in the elastic shock the final speed of the tennis ball is approximately 2 vo, we can calculate the maximum height

m g h = 1/2 m (2v₀)²

h = 2 v₀²/g

To reconcile this with the conservation of energy we must calculate the energy for the tennis ball at two points, the first when the crash with the tennis ball ends and at the end point at its maximum height.