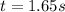Answer:
a)
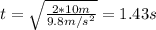
b)
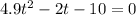
And we can use the quadratic formula to solve it:
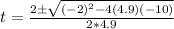
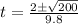
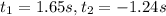
And since the time can't be negative the correct option would be
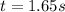
Explanation:
For this case we can use the following kinematics formulas:

For this case we assume that the only acceleration is the gravity a = g =9.8 m/s^2. And for this case we can assume that the reference point is
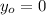 and the final height would be
and the final height would be
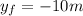 since is below the initial point.
since is below the initial point.
Teh acceleration would be a=-g, since the gravity is acting dowward, we assume that the initial velocity is 0, so then we have everything to replace and we got:
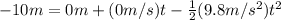
And solving for t we got:
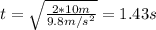
For the second part assuming that We have an initial vertical speed of
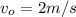 we have the following equation:
we have the following equation:

And we have this quadratic equation:
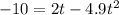
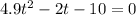
And we can use the quadratic formula to solve it:
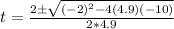
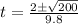
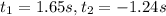
And since the time can't be negative the correct option would be