Question

A local grocery store chain has a sushi stand. That sushi stand makes samples for store customers to entice customers to purchase sushi while shopping. The number of customers that pass by the stand and sample sushi per hour is Poisson distributed with a mean of 14. What is the probability that the inter-arrival time between two customers is less than or equal to 2 minutes

Answer 1

Answer: 0.99822

Explanation:

Our inter-arrival time follows Poisson distribution with parameter 14 which is in hour so first we have to calculate this in minutes as we have to calculate probability in minutes.

So converting 14 into minutes will give
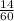`(14)/(60)`=0.233

Let X=inter-arrival time between two customers

and here
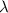`\lambda` = 0.233

Probability(X is less than or equal to 2 minutes) = P(X=0) + P(X=1) + P(X=2)

Now the Poisson distribution has PDF =
`(\exp ^(-\lambda )* \lambda ^(X))/(X!)`

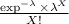
So P(X = 0) =
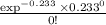`(\exp ^(-0.233)* 0.233^(0))/(0!)` = 0.79215

P(X= 1) =
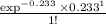`(\exp ^(-0.233)* 0.233^(1))/(1!)` = 0.18457

P(X=2) =
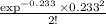`(\exp ^(-0.233)* 0.233^(2))/(2!)` = 0.02150

Now adding all three probability gives = 0.79215 +0.18457 + 0.02150=0.99822