Option B is the correct answer.
Explanation:
We need to find average value of
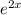 in [2,4]
in [2,4]
Area of
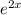 in [2,4] is given by
in [2,4] is given by
![\int_(2)^(4)e^(2x)dx=(1)/(2)* \left [ e^(2x)\right ]^4_2\\\\\int_(2)^(4)e^(2x)dx=(1)/(2)*(e^8-e^4)=1463.18](https://img.qammunity.org/2021/formulas/mathematics/middle-school/am5mp6nd6ag8w07xzrfrd3lcz2a6ggdrkd.png)
Area of
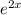 in [2,4] = 1463.18
in [2,4] = 1463.18
Difference = 4 - 2 = 2
Average value = Area of
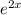 in [2,4] ÷ Difference
in [2,4] ÷ Difference
Average value = 1463.18 ÷ 2
Average value = 731.59
Option B is the correct answer.