Question

A rocket explodes into two fragments, one 25 times heavier than the other. The magnitude of the momentum change of the lighter fragment is

Answer 1

The same as the momentum change of the heavier fragment.

(b) is correct option.

Step-by-step explanation:

Given that,

A rocket explodes into two fragments, one 25 times heavier than the other.

`m_(2)=25m_(1)`

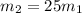
Suppose, given options are

a.)
`(1)/(4)` as great as the momentum change of the heavier fragment.

b.) The same as the momentum change of the heavier fragment.

c.)
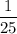`(1)/(25)` as great as the momentum change of the heavier fragment.

d.) 5 times as great as the momentum change of the heavier fragment.

e.) 25 times as great as the momentum change of the heavier fragment.

The initial momentum of the system is zero.

We need to calculate the final momentum

Using formula of momentum

`P_(f)=m_(1)v_(1)+m_(2)v_(2)`

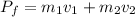
Here,
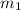`m_(1)`=mass of the lighter fragments

`m_(2)`=mass of the heavier fragments

Lighter weight has the greater velocity and heavier weight has less velocity.

According to the conservation of momentum

`P_(i)=P_(f)`

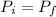
The change in momentum of heavier and lighter mass is same

Hence, The same as the momentum change of the heavier fragment.