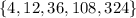The sequence defines a function
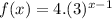
Domain :

Range :
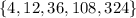
Step-by-step explanation:
A sequence defines a function if it is the set of natural numbers.
Thus, the function is given by
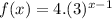
The sequence can be determined by substituting the values for x.
For
 ,
,

For
 ,
,
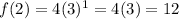
For
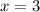 ,
,
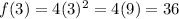
For
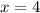 ,
,
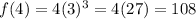
For
 ,
,
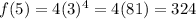
Thus, from these the domain and range of a function can be determined.
The domain of a function is the set of independent values, which are generally the x-coordinates.
Domain of a function is

The range of a function is the set of dependent values obtained by substituting the values for x.
Range of a function is