Question

Find the x-coordinates of any relative extrema and inflection point(s) for the function f(x)= 6x^1/3 + 3x^4/3. You must justify your answer using an analysis of f'(x) and f''(x)

My work so far
F'(x) =2/(x^2/3) + 4x^1/3
​

Answer 1

x-coordinates of relative extrema =
`(-1)/(2)`

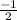
x-coordinates of the inflexion points are 0, 1

Explanation:

`f(x)=6x^{(1)/(3)}+3x^{(4)/(3)}`

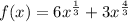
Differentiate with respect to x

`f'(x)=6\left ( (1)/(3) \right )x^{(-2)/(3)}+3\left ( (4)/(3) \right )x^{(1)/(3)}=\frac{2}{x^{(2)/(3)}}+4x^{(1)/(3)}`

`f'(x)=0\Rightarrow \frac{2}{x^{(2)/(3)}}+4x^{(1)/(3)}=0\Rightarrow x=(-1)/(2)`

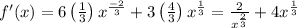
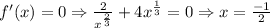
Differentiate f'(x) with respect to x

`f''(x)=2\left ( (-2)/(3) \right )x^{(-5)/(3)}+(4)/(3)x^{(-2)/(3)}=\frac{-4x^{(2)/(3)}+4x^{(5)/(3)}}{3x^{(2)/(3)}x^{(5)/(3)}}\\f''(x)=0\Rightarrow \frac{-4x^{(2)/(3)}+4x^{(5)/(3)}}{3x^{(2)/(3)}x^{(5)/(3)}}=0\Rightarrow x=1`

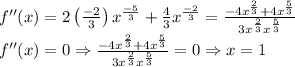
At x =
`(-1)/(2)`,

`f''\left ( (-1)/(2) \right )=\frac{4\left ( -1+4\left ( (-1)/(2) \right ) \right )}{3\left ( (-1)/(2) \right )^{(5)/(3)}}>0`

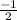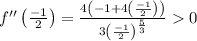
We know that if
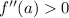`f''(a)>0` then x = a is a point of minima.

So,
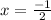`x=(-1)/(2)` is a point of minima.

For inflexion points:

Inflexion points are the points at which f''(x) = 0 or f''(x) is not defined.

So, x-coordinates of the inflexion points are 0, 1