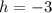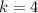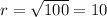Question

A circle has the equation 2x²+12x+2y²−16y−150=0.

What are the coordinates of the center, and what is the length of the radius?
A. The coordinates at the center are (6,-8), and the length of the radius is 10 units.
B. The coordinates of the center are (-3,4), and the length of the radius is 10 units.
C. The coordinates of the center are (-6,8), and the length of the radius is 10 units.
D. The coordinates of the center are (3,-4), and the length of the radius is 10 units.

Answer 1

Answer: B. The coordinates of the center are (-3,4), and the length of the radius is 10 units.

Explanation:

The equation of a circle in the center-radius form is:

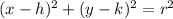`(x-h)^(2) +(y-k)^(2)=r^(2)` (1)

Where
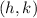`(h,k)` are the coordinates of the center and
`r` is the radius.

Now, we are given the equation of this circle as follows:

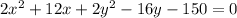`2x^(2)+12x+2y^(2)-16y-150=0` (2)

And we have to write it in the format of equation (1). So, let's begin by applying common factor 2 in the left side of the equation:

`2(x^(2)+6x+y^(2)-8y-75)=0` (3)

Rearranging the equation:

`x^(2)+6x+y^(2)-8y=75` (4)

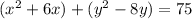`(x^(2)+6x)+(y^(2)-8y)=75` (5)

Now we have to complete the square in both parenthesis, in order to have a perfect square trinomial in the form of
`(a\pm b)^(2)=a^(2)\pm+2ab+b^(2)`:

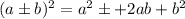For the first parenthesis:

`x^(2)+6x+b^(2)`

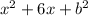
We can rewrite this as:

`x^(2)+2(3)x+b^(2)`

Hence in this case
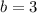`b=3` and
`b^(2)=9`:

`x^(2)+2(3)x+3^(2)=x^(2)+6x+9=(x+3)^(2)`

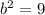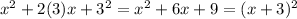
For the second parenthesis:

`y^(2)-8y+b^(2)`

We can rewrite this as:

`y^(2)-2(4)y+b^(2)`

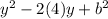
Hence in this case
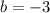`b=-3` and
`b^(2)=9`:

`y^(2)-2(4)y+4^(2)=y^(2)-8y+16=(y-4)^(2)`

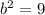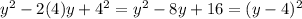
Then, equation (5) is rewritten as follows:

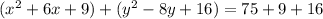`(x^(2)+6x+9)+(y^(2)-8y+16)=75+9+16` (6)

Note we are adding 9 and 16 in both sides of the equation in order to keep the equality.

Rearranging:

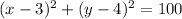`(x-3)^(2)+(y-4)^(2)=100` (7)

At this point we have the circle equation in the center radius form
`(x-h)^(2) +(y-k)^(2)=r^(2)`

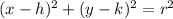
Hence:

`h=-3`

`k=4`

`r=√(100)=10`