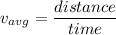Question

The velocity of a particle traveling in a straight line is given by v = (6t - 3t²) m/s, where t is in seconds. If s = 0 when t = 0, determine the particle’s deceleration and position when t = 3s. How far has the particle traveled during the 3-s time interval, and what is its average speed?

Answer 1

given,

v = (6 t - 3 t²) m/s

we know,

`v = (dx)/(dt)`

`a = (dv)/(dt)`

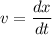
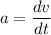
position of the particle

`dx = v dt`

integrating both side

`\int dx = (6t - 3 t^2)\int dt`

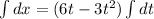
x = 3 t² - t³

Position of the particle at t= 3 s

x = 3 x 3² - 3³

x = 0 m

now, particle’s deceleration

`a = (dv)/(dt)`

`a = (d)/(dt)(6t - 3 t^2)`

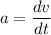
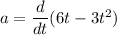
a = 6 - 6 t

at t= 3 s

a = 6 - 6 x 3

a = -12 m/s²

distance traveled by the particle

x = 3 t² - t³

at t = 0 x = 0

t = 1 s , x = 3 (1)² - 1³ = 2 m

t = 2 s , x = 3(2)² - 2³ = 4 m

t = 3 s , x = 0 m

total distance traveled by the particle

D = distance in 0-1 s + distance in 1 -2 s + distance in 2 -3 s

D = 2 + 4 + 2 = 8 m

average speed of the particle

`v_(avg) = (distance)/(time)`

`v_(avg) = (8)/(3)`

`v_(avg) =2.67\ m/s`