Answer:
4,690,625,500 different samples are possible.
Explanation:
The order of coins in the sample is not important. For example, if our box is:
A-B-C-D-E-F
It is the same as
F-A-B-C-D-E
So we use the combinations formula to find how many different samples are possible.
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

In this problem, we have that:
Number of combinations of 6 from 125. So

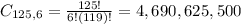
4,690,625,500 different samples are possible.