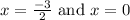Question

Solve the absolute value equation. |4x+3|=3
sos

Answer 1

The solution for absolute value equation |4x + 3| = 3 is:

`x = (-3)/(2) \text{ and } x = 0`

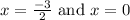
Solution:

Absolute value equations are equations where the variable is within an absolute value operator

Given absolute value equation is:

`|4x+3|=3`

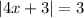
The absolute value of a number depends on the number's sign

Clear the absolute-value bars by splitting the equation into its two cases, one for the Positive case and the other for the Negative case.

The Absolute Value term is |4x + 3|

For the Negative case we use -(4x + 3)

For the Positive case we use (4x + 3)

Solve the Negative Case

-(4x + 3) = 3

-4x - 3 = 3

-4x = 3 + 3

-4x = 6

Divide both sides by -4

`x = (-6)/(4)\\\\x = (-3)/(2)`

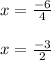
Solve the Positive Case

(4x + 3) = 3

4x + 3 = 3

Move the constants to right

4x = 3 - 3

4x = 0

x = 0

Thus two solutions were found :
`x = (-3)/(2) \text{ and } x = 0`