Question

Consider an object of mass m moving along a frictionless surface and attached to a wall by a spring. If we let y(t) denote the spring's displacement from equilibrium, and we assume y(t) is small, then the motion can often be modeled by an equation of the form my" = -kıy+ k3y^3, where ki is Hooke’s constant and the term k3y3 is a nonlinear correction corresponding with the fact that the spring will weaken if either strongly stretched or strongly compressed. Find the dimensions of kį and k3 and nondimensionalize this equation.

Answer 1

The dimensions of Ki are N/m while the dimension of K3 is N/m³. The Nondimensional equation is:

`(d^2Y)/(d\tau^2) -Y-Y^3=0`

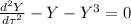
with the substitution:

`y=y_0Y \displaystyle\leftrightarrow y_0=\sqrt{(k_i)/(k_3)}`

`t=t_0\tau \leftrightarrow \tau=\displaystyle\sqrt{(m)/(k_i) }`

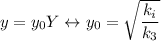
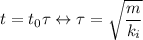
Explanation:

To determine the dimensions of the constant we first see the first part of the equation, knowing that each term has to have the same dimension.

The first term is mass multiplied with acceleration, this means that the dimension of each term is the unit of force, Newtons.

The second term is distance multiplied with ki. If the term has to have the force dimension, ki dimensions must be N/m.

The third term is distance to the cube multiplied with k3. If the term has to have the force dimension, k3 dimensions must be N/m³.

For the process of Nondimensionalization, we first make the substitution of the main variables (in this case t of time and y of distance) for nondimensional ones (in this case Y and τ):

`y=y_0Y`

`t=t_0\tau`

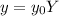
Where y₀ and t₀ are the characteristic units used to scale the equation.

Substituted in the original equation:

`m(d^2y)/(dt^2) -k_iy-k_3y^3=0\\m(y_0)/(t_0^2) (d^2Y)/(d\tau^2) -k_iy_0Y-k_3y_0^3Y^3=0`

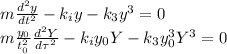
Now we clear the highest degree term of the differential equation:

`\displaystyle(d^2Y)/(d\tau^2) -(k_it_0^2)/(m) Y-(k_3t_0^2y_0^2)/(m) Y^3=0\\(d^2Y)/(d\tau^2) -A Y-B Y^3=0`

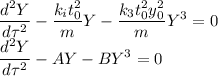
Now we need that coefficients A and B to be the unit without any dimension, Therefore:

`\displaystyle A=1=(k_it_0^2)/(m) \leftrightarrow t_0=\sqrt{(m)/(k_i)} \\B=1=(k_3t_0^2y_0^2)/(m)=(k_3y_0^2)/(k_i) \leftrightarrow y_0=\sqrt{(k_i)/(k_3)}`

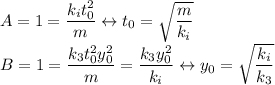
With this characteristic units the equation is Nondimensional.