Question

For the data set: 0.09, 0.10, 0.11, 0.13, 0.09, 0.11, 0.10, 0.07 Which variance would describe the precision of the data? Group of answer choices 0.00031 0.00036 0.00025 0.00038

Answer 1

Answer:0.00031

Explanation:

Firstly find the mean

Let m be mean

Mean= sum/ n

M=(0.09+0.10+0.11+0.13+0.09+0.11+0.10+0.07) / 8

M= 0.10

Variance= |x-m|^2 / n-1

For 1st: |0.09-0.10|^2 = 0.0001

For 2nd: |0.10-0.10|^2 = 0.000

For 3rd: |0.11-0.10|^2 = 0.0001

For 4th: |0.13-0.10|^2= 0.0009

For 5th: |0.09-0.10|^2 = 0.0001

For 6th: |0.11-0.10| ^2= 0.0001

For 7th: |0.10-0.10|^2= 0.0000

For 8th: |0.07-0.10|^2 = 0.0009

Variance= |x-m|^2 / n-1

Variance=0.0022 / 7

Variance= 0.00031

Answer 2

`s^2 =((0.09-0.1)^2+(0.1-0.1)^2+(0.11-0.1)^2+(0.13-0.1)^2+(0.09-0.1)^2+(0.11-0.1)^2+(0.1-0.1)^2+(0.07-0.1)^2)/(8-1)=0.000314`

So then the best answer would be:

0.00031

Explanation:

We have the followinf dataset:

0.09, 0.10, 0.11, 0.13, 0.09, 0.11, 0.10, 0.07

For this case we want to calculate the sample variance. But in order to calculate it we need to find first the sample mean given by:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And if we replace we got:

`\bar X = (0.09+0.1+0.11+0.13+0.09+0.11+0.1+0.07)/(8)=0.1`

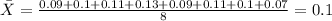
Now the sample variance can be calculated with the following formula:

`s^2 = (\sum_(i=1)^n (x_i -\bar X)^2)/(n-1)`

And if we replace we got:

`s^2 =((0.09-0.1)^2+(0.1-0.1)^2+(0.11-0.1)^2+(0.13-0.1)^2+(0.09-0.1)^2+(0.11-0.1)^2+(0.1-0.1)^2+(0.07-0.1)^2)/(8-1)=0.000314`

So then the best answer would be:

0.00031