Question

Choose the system of equations which matches the following graph: (1 point) a line includes points 0 comma negative 1 and 5 comma negative 2. A line includes points 5 comma negative 2 and 0 comma negative 5 3x + 5y = −25 x−5y = 5 3x + 5y = −25 x + 5y =−5 3x − 5y = 25 x + 5y =−5 3x − 5y = 25 x−5y = 5

Answer 1

The system of equations is

`x+5y=-5`

`3x-5y=25`

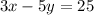
Explanation:

step 1

Find the equation of a line that passes through the points

(0,-1) and (5,-2)

Find the slope

`m=(-2+1)/(5-0)=-(1)/(5)`

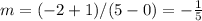
The equation of the line in slope intercept form is

`y=mx+b`

we have

`m=-(1)/(5)`

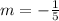
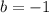`b=-1` ---> the y-intercept is given

substitute

`y=-(1)/(5)x-1`

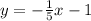
Convert to standard form

Multiply by 5 both sides

`5y=-x-5`

`x+5y=-5` ----> equation 1

step 2

Find the equation of a line that passes through the points

(5,-2) and (0,-5)

Find the slope

`m=(-5+2)/(0-5)=(3)/(5)`

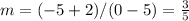
The equation of the line in slope intercept form is

`y=mx+b`

we have

`m=(3)/(5)`

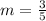
`b=-5` ---> the y-intercept is given

substitute

`y=(3)/(5)x-5`

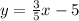
Convert to standard form

Multiply by 5 both sides

`5y=3x-25`

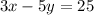`3x-5y=25` ----> equation 2

therefore

The system of equations is

`x+5y=-5`

`3x-5y=25`

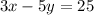
The solution of the system is the point (5,-2)

Because is a common point both graphs