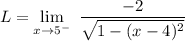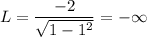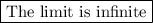Question

Can somebody help me with this inverse trigonometric limit?

Answer 1

The limit is infinite

Explanation:

L'Hopital's Rule

It's used when we are computing a given rational limit and the result is an indeterminate expression like 0/0. If the limit has is rational function with f(x) in the numerator and g(x) in the denominator, then

`\displaystyle \lim _(x\rightarrow a)(f(x))/(g(x))=\lim _(x\rightarrow a)\ (f'(x))/(g'(x))`

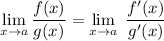
We need to compute

`\displaystyle L= \lim _(x\rightarrow 5^-)\ (2\ arccos(x-4))/(x-5)=(2\ arccos\ 1)/(5-5)=(0)/(0)`

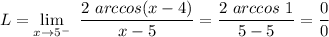
Since the result is an indetermination, we use L'Hopital's rule, by computing f'(x) and g'(x) as follows

`\displaystyle f(x)=2\ arccos(x-4)`

`\displaystyle g(x)=x-5`

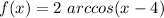
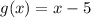
Recall the derivative of the arccos function is

`\displaystyle [arccos\ u]'=-(-u')/(√(1-u^2))`

Thus:

`\displaystyle f'(x)=[2arccos(x-4)]'=(-2(x-4)')/(√(1-(x-4)^2))`

`\displaystyle f'(x)=(-2)/(√(1-(x-4)^2))`

`\displaystyle g'(x)=1`

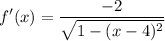
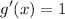
Replacing into the original limit, we have

`\displaystyle L=\lim _(x\rightarrow 5^-)\ (-2)/(√(1-(x-4)^2))`

`\displaystyle L=(-2)/(√(1-1^2))=-\infty`

`\boxed{\text{The limit is infinite}}`