Question

Two triangles are similar. The perimeter of the smaller one is 16. The ratio of the corresponding sides is 2:5. The sides of the smaller triangle are 2,6 and 8. What is the perimeter of the larger triangle?

Answer 1

Perimeter of larger triangle is 40.

Explanation:

Given:

Perimeter of smaller circle = 16

Ratio of corresponding side = 2:5

We need to find the perimeter of the larger triangle.

Solution:

Let the perimeter of the larger triangle be 'x'.

Therefore by theorem which states that;

" When a triangle have scale factor a:b then the ratio of the perimeters is a:b".

Here Ratio is 2:5, so we can say by theorem, Ratio of perimeters is 2:5

framing in equation form we get;

`\frac{\textrm{Perimeter of smaller triangle}}{\textrm{Perimeter of Larger triangle}}=(2)/(5)`

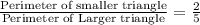
Substituting the values we get;

`(16)/(x)=(2)/(5)`

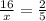
By Cross multiplication we get;

`16* 5=2x\\\\80=2x`

Dividing both side by 2 we get;

`(80)/(2)=(2x)/(2)\\\\x=40`

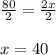
Hence Perimeter of larger triangle is 40.