Question

2. Find the equation of the line tangent to the curve with parametric equations x = 4 cos θ y = 9 sin θ at θ = π 4 .

Answer 1

`9x+4y=36√(2)`

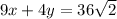
Explanation:

The given equations are

`x=4\cos \theta`

`y=9\sin \theta`

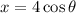
Differentiate with respect to θ .

`(dx)/(d\theta)=-4\sin \theta`

`(dy)/(d\theta)=9\cos \theta`

`(dy)/(dx)=(dy)/(d\theta)* (d\theta)/(dx)=(9\cos \theta)/(-4\sin \theta)=-(9)/(4)\cot \theta`

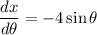
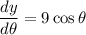
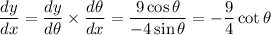
At θ = π/4 ,

`(dy)/(dx)=-(9)/(4)\cot ((\pi)/(4))=-(9)/(4)`

`x=4\cos ((\pi)/(4))=4((1)/(√(2)))=(4)/(√(2))`

`y=9\sin ((\pi)/(4))=9((1)/(√(2)))=(9)/(√(2))`

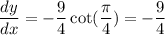
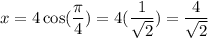
Slope of the tangent line is -9/4 and point of tangency is
`((4)/(√(2)),(9)/(√(2)))`.

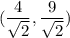The equation of tangent line is

`y-y_1=m(x-x_1)`

where, m is slope.

`y-(9)/(√(2))=-(9)/(4)(x-(4)/(√(2)))`

`y-(9)/(√(2))=-(9)/(4)(x)+(9)/(√(2))`

`(9)/(4)(x)+y=(9)/(√(2))+(9)/(√(2))`

`(9)/(4)(x)+y=(18)/(√(2))`

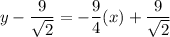
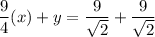
Multiply both sides by 4.

`9x+4y=(72)/(√(2))`

`9x+4y=36√(2)`

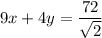
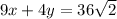
Therefore, the equation of the line tangent is
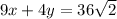`9x+4y=36√(2)`.