Question

Suppose X and Y are the scores that a SIE student will receive, respectively, on the verbal and math portions of a test. Further suppose that X and Y are both Nor(70, 100) and that Cov(X, Y ) = 25. Find the probability that the total score, X + Y , will exceed 150. Assume that X + Y is normal, and use the Z-table.

Answer 1

Answer: 0.71142

Explanation:

Mean of X and Y is given 70 each and Variance of X and Y is given 100 each

Let Z = X+Y

Mean of Z = Mean of X + Mean of Y

= 70 + 70 = 140

Variance of Z = Variance(X+Y) = Co Variance(X+Y,X+Y)

= Variance(X) + Variance(Y) + 2 Co variance(X+Y)

= 100 + 100 + 2(25) = 250

So Z has mean 140 and standard deviation =
`√(250)`

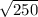
To calculate Probability of P(X+Y>150) = P(Z>150) = 1 - P(Z<=150)

P(X+Y<=150) = P(Z<=
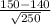`(150-140)/(√(250))` ) = P(Z<=0.63245)

Now using z table to calculate this probability we get P(Z<=0.63245) = 0.28858 { using interpolation }

Now P(Z>150) = 1 - 0.28858 = 0.71142