Question

Determine the approximate value of x.

2.045

3.264

6.736

Answer 1

x = 6.736

Solution:

The image attached below.

Given ∠A = 80°, ∠C = 40° and side a = 5.

Let us first find the measure of ∠B.

Sum of the angles of a triangle = 180°

⇒ ∠A + ∠B + ∠C = 180°

⇒ 80° + ∠B + 40° = 180°

⇒ ∠B + 120° = 180°

⇒ ∠B = 180° – 120°

⇒ ∠B = 60°

Let us find the side c using sine law,

`(b)/(\sin B)=(c)/(\sin C)`

⇒
`(x)/(\sin 60^(\circ))=(5)/(\sin 40^(\circ))`

⇒
`x=(5* \sin 60^(\circ))/(\sin 40^(\circ))`

⇒
`x=(5 * (√(3))/(2))/(0.6428)`

⇒
`x=\frac{5 * √(3)}{2* {0.6428}}}`

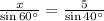
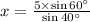
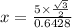
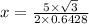
⇒ x = 6.736

Hence, the value of x is 6.736.