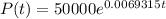Question

Some time in the future a human colony is started on Mars. The colony begins with 50000 people and grows exponentially to 200000 in 200 years. Give a formula for the size of the human population on Mars as a function of t

Answer 1

`P(t) = 50000 e^(0.0069315 t)`

Explanation:

For this case since the population follows an exponential model we have the general equation:

`P(t) = P_o e^(rt)`

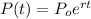
Where P(t) represent the population at time t. t represent the years since the starting year.

r represent the growth/dcay constant rate

For this case we have the initial condition given :
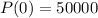`P(0) = 50000` and if we replace this into the general equation we have:

`50000 = P_o e^(r*0) = P_o`

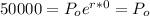
And the equation would be:

`P(t) = 50000 e^(rt)`

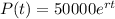
Now we can use the second condition given
`P(200) =200000` and replacing into the general formula we got:

`200000= 50000 e^(200t)`

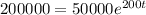
We can divide both sides by 50000 and we got:

`4 = e^(200t)`

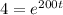
Now we can apply natural log on both sides:

`ln(4) = 200t`

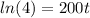
And then:

`t = (ln(4))/(200)=0.0069315`

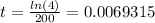
So then our final equation would be given by:

`P(t) = 50000 e^(0.0069315 t)`