Question

To what tension (in newtons) must you adjust the screw so that a transverse wave of wavelength 3.33 cm makes 621 vibrations per second?

Answer 1

T=9.4 N

Step-by-step explanation:

We are given that

Mass of wire,m=16.5 g=
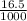`(16.5)/(1000)`kg

1 kg=1000g

Length of wire,l=75 cm=
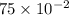`75* 10^(-2)`m

1 m=100 cm

Wavelength of transverse wave=
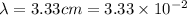`\lambda=3.33 cm=3.33* 10^(-2)`m

Frequency=
`621 Hz`

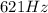
Mass per unit length=
`m_l=(m)/(l)=(16.5)/(1000* 75* 10^(-2))=0.022 kg/m`

`\\u=(v)/(\lambda)`

`v=\\u \lambda`

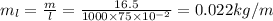
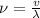
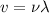
Where
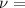`\\u=`frequency of wave

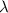`\lambda`=Wavelength of wave

Speed of wave=v

Using the formula

`v=3.33* 10^(-2)* 621=20.7m/s`

`v=\sqrt{(T)/(m_l)}`

`v^2=(T)/(m_l)`

`T=v^2m_l`

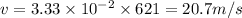
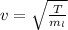
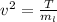
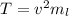
Using the formula

`T=(20.7)^2* 0.022=9.4N`

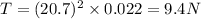
Hence, the tension,T=9.4 N