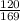The value of sin(2x) is
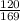
Step-by-step explanation:
Given that
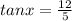
The formula for
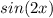 is
is
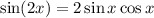
Since,
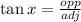
Also, it is given that
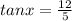
Thus,
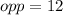 and
and
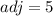
To find the hypotenuse, let us use the pythagoras theorem,
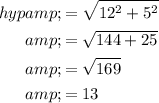
Now, we can find the value of sin x and cos x.
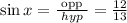
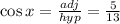
Now, substituting these values in the formula for sin 2x, we get,
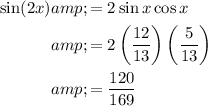
Thus, the value of sin(2x) is