Answer:
The approximate are of the inscribed disk using the regular hexagon is

Explanation:
we know that
we can divide the regular hexagon into 6 identical equilateral triangles
see the attached figure to better understand the problem
The approximate area of the circle is approximately the area of the six equilateral triangles
Remember that
In an equilateral triangle the interior measurement of each angle is 60 degrees
We take one triangle OAB, with O as the centre of the hexagon or circle, and AB as one side of the regular hexagon
Let
M ----> the mid-point of AB
OM ----> the perpendicular bisector of AB
x ----> the measure of angle AOM
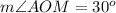
In the right triangle OAM
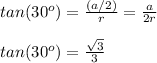
so
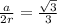
we have
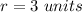
substitute
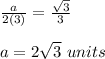
Find the area of six equilateral triangles
![A=6[(1)/(2)(r)(a)]](https://img.qammunity.org/2021/formulas/mathematics/college/wlvr5hdqwd8l2t1h7fh190a0of8isd45po.png)
simplify
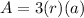
we have
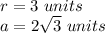
substitute
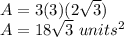
Therefore
The approximate are of the inscribed disk using the regular hexagon is
