Question

Assume that trees are subjected to different levels of carbon dioxide atmosphere with 7% of the trees in a minimal growth condition at 370 parts per million (ppm), 10% at 440 ppm (slow growth), 49% at 550 ppm (moderate growth), and 34% at 670 ppm (rapid growth). What is the mean and standard deviation of the carbon dioxide atmosphere (in ppm) for these trees

Answer 1

Answer: The mean and standard deviation are 567.2 and 89.88 resp.

Explanation:

Since we have given that

For 370 parts per million = 7% = 0.07

For 440 parts per million = 10% = 0.10

For 550 parts per million = 49% = 0.49

For 670 parts per million = 34% = 0.34

So, Mean of the carbon dioxide atmosphere for these trees would be

`E[x]=370* 0.07+440* 0.1+550* 0.49+670* 0.34=567.2`

And

`E[x^2]=370^2* 0.07+440^2* 0.1+550^2* 0.49+670^2* 0.34=329794`

So, Variance would be

`Var\ x=E[x^2]-E[x]^2=329794-567.2^2=8078.16`

So, the standard deviation would be

`\sigma=√(8078.16)=89.88`

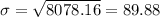
Hence, the mean and standard deviation are 567.2 and 89.88 resp.