Question

A bare helium nucleus has two positive charges and a mass of 6.64×10−27kg(a) Calculate its kinetic energy in joules at 2.00% of the speed of light.(b) What is this in electron-volts? (c) What voltage would be needed to obtain this energy?

Answer 1

To solve this problem we will apply the concepts related to kinetic energy and energy conservation. The kinetic energy will be expressed in terms of mass and speed, as well as load and voltage. From this last expression we will find the charges by electron and by Helium nucleus.

a ) Kinetic Energy is given as

`KE = (1)/(2) mv^2`

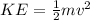
Replacing with our values we have that

`KE = (1)/(2) (6.64*10^(-27))(2.0\% (3.00*10^8))^2`

`KE = 1.1935*10^(-13)J`

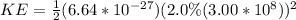
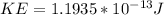
Therefore the kinetic energy of the helium nucleus is
`1.1935*10^(-13)J`

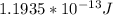
PART B) Now for calculate the electron volts we use the kinetic energy as a expression between the charge and the voltage, that is

`KE = qV`

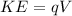
Here,

q = Charge of an electron

V = Voltage

Rearranging to find the potential we have,

`V = (KE)/(q)`

`V = (1.19*10^(-13))/(1.6*10^(-19))`

`V = 743750eV`

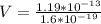
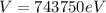
Therefore the kinetic energy in electron vols is
`743750eV`

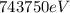
PART C) Applying the same relationship but now using the Helium core load, we will have to

`KE = QV`

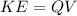
Here,

Q = Charge of a helium nucleus

V = Voltage

Rearranging to find the potential we have

`V = (KE)/(Q)`

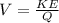
But we need to note that the charge is equal to the number of charge for the unit charge, then

`Q = \text{No. Charge} * \text{Unit Charge}`

`Q = (2)(1.6*10^(-19)C)`

`Q = 3.2*10^(-19)C`

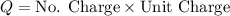
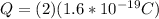
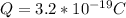
Now replacing we have that

`V= (1.19*10^(-13))/(32*10^(-19))`

`V = 371875V`

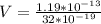
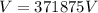
Therefore the voltage applied is 371875V