Answer:
Option A) m∠RNS=27°
Explanation:
We know that
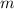 ∠UNR = 180°. This tells us that the Sum of the enclosed angles should equal 180°, by trigonometry. So the enclosed angles are:
∠UNR = 180°. This tells us that the Sum of the enclosed angles should equal 180°, by trigonometry. So the enclosed angles are:
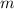 ∠RNS =
∠RNS =
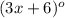
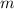 ∠SNT=
∠SNT=
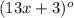
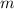 ∠TNU=
∠TNU=

Now let us add all the angles and solve for the value of
 as follow:
as follow:
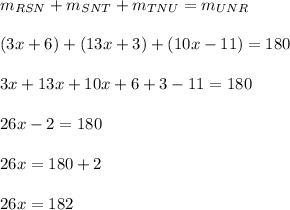
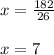
Now lets plug in the value into the expression for angle
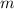 ∠RNS to find the angle as:
∠RNS to find the angle as:
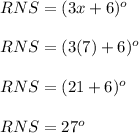
Thus Option A. is the correct answer.