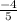Question

If cos x= -4/5 and pi Please someone can help me?

Answer 1

`sin(x+(\pi )/(2)) = (-4)/(5)`

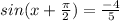
Explanation:

Given
`cos x = (-4)/(5)`

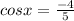
given 'x' lies in
`\pi <x<(3\pi )/(2)`

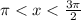
we know that sin(A+B) = sin A cos B + cos A sin B

`sin(x+(\pi )/(2) )` =
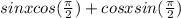`sin x cos((\pi )/(2) )+ cos x sin((\pi )/(2) )` .........................(1)

we will use trigonometry formulas

`cos((\pi )/(2)) = 0`

`sin((\pi )/(2) )=1`

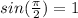
sin x is negative in third and fourth quadrant (
`\pi <x<(3\pi )/(2)`)

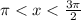find sin x value

using trigonometry formulas
`sin^(2) x+cos^2 x=1`

`sin^(2)x = 1 - cos^2 x`

=
`1-((-4)/(5)))^2`

`sin^2 x = 1 - (16)/(25)`

`sin x = \sqrt{(25-16)/(25) }`

sin x =
`\sqrt{(9)/(25) }`

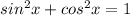
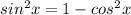
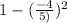
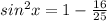
`sin x = (3)/(5)`

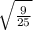
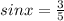
in third and fourth quadrant is negative so sin x=
`(-3)/(5)`

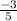
now equation (1), we get solution

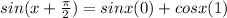
`sin(x+(\pi )/(2)) = sin x ( 0 ) + cos x (1)`

=
`(-4)/(5)`