Question

Let f(x) = x + 3 and g(x) = 1/x The graph of (gºf)(x) is shown below what is the range of ( gof) (x) .

Answer 1

The range of the function
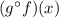`(g\°f)(x)` is

B. is all real numbers except
`y=0`

Explanation:

Given functions:

`f(x)=x+3`

`g(x)=(1)/(x)`

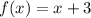
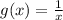
To find the range of
`(g\°f)(x)`.

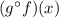Solution:

In order to find
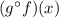`(g\°f)(x)` , we will plugin
`f(x)` in function
`g(x)`.

`(g\°f)(x)=g(f(x))`

`(g\°f)(x)=(1)/(x+3)`

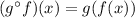
The graph of the function
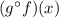`(g\°f)(x)` shows that

1) As
`x` approaches -3 (but never touches the line
`x=-3`),
`y` tends to positive or negative infinity.

2) As
`y` approaches 0 (but never touches the line
`y=0`) ,
`x` tends to positive or negative infinity.

Thus, the range of the function is all real numbers except
`y=0`