Answer with explanation:
Let
 be the average starting salary ( in dollars).
be the average starting salary ( in dollars).
As per given , we have

Since
 is left-tailed , so our test is a left-tailed test.
is left-tailed , so our test is a left-tailed test.
WE assume that the starting salary follows normal distribution .
Since population standard deviation is unknown and sample size is small so we use t-test.
Test statistic :
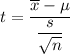 , where n= sample size ,
, where n= sample size ,
 = sample mean , s = sample standard deviation.
= sample mean , s = sample standard deviation.
Here , n= 15 ,
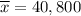 , s= 225
, s= 225
Then,
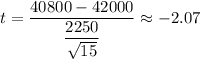
Degree of freedom = n-1=14
The critical t-value for significance level α = 0.01 and degree of freedom 14 is 2.62.
Decision : Since the absolute calculated t-value (2.07) is less than the critical t-value., so we cannot reject the null hypothesis.
Conclusion : We do not have sufficient evidence at 1 % level of significance to support the claim that the average starting salary of the graduates is significantly less that $42,000.