Question

Brady rode his bike 70 miles in 4 hours. He rode at an average speed of 17 miles per hour for t hours and at an average rate of speed of 22 miles per hour for the rest of the time. How long did Brady ride at the slower speed? Use the variable t to represent the time, in hours, Brady rode at 17 miles per hour.

Answer 1

Brady rides at slower speed which is 17 miles/hours for 3 hours and 36 minutes.

Explanation:

Given:

Brady rode 70 miles in 4 hours.

For
`t` hours he rode at the average rate of 17 miles/hour

For rest of the time he rode at the average rate of 22 miles per hour.

To find the time Braady rode at the slower speed.

Solution:

Total time of riding = 4 hours

Time for which Brady rides at 17 miles/ hour =
`t` hours

Distance covered in
`t` hours =
`Speed* time=17* t =17t\ miles`

So, time for which Brady rides at 22 miles/ hour =
`(4-t)` hours

Distance covered in
`(4-t)` hours =
`Speed* time=22*(4-t) =(88-22t)\ miles`

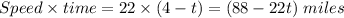
Total distance can be given as:

⇒
`17t+88-22t`

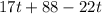
Simplifying.

⇒
`-5t+88`

Total distance given =70 miles.

Thus, the equation to find
`t` can be given as:

`-5t+88=70`

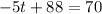
Subtracting both sides by 88.

`-5t+88-88=70-88`

`-5t=-18`

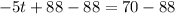
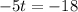
Dividing both sides by -5.

`(-5t)/(-5)=(-18)/(-5)`

∴
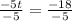
`t=3.6` hours

`3.6\ hours = 3\ hour+ (0.6* 60)\ minutes = 3\ hour\ 36\ minutes`

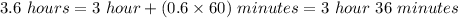
Thus, Brady rides at slower speed which is 17 miles/hours for 3 hours and 36 minutes.