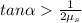Question

A uniform ladder of mass m and length L stands on a floor at angle α, leaning against a frictionless wall. The static coefficient of friction between the ladder and the floor is µs. Calculate the minimum value of the angle α for which the ladder remains in equilibrium.

Answer 1

To solve this problem it will be necessary to apply the equilibrium conditions. At the same time, it is necessary to make a free body diagram that allows clarifying the origin of the forces with their respective components used to generate the system of equations that allow us to determine the value of the necessary Angle.

As show in free body diagram we have that

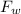`F_w` = Force due to wall

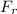`F_r`= Frictional force

N = Normal Force

For equilibrium the moments about point A must be zero, then

`\sum M_A = 0`

`(F_w sin\theta)(L)-(mgcos\alpha)((L)/(2))=0`

`F_w = (mg)/(2tan\alpha)`

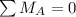
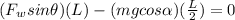
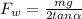
And similarly the equilibrium with the force show us that,

`\sum F_x = 0`

`N = mg`

`\sum F_y = 0`

`F_w = F_r = \mu_s N`

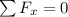
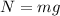
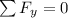
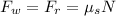
From above equation and replacing we have then

`(mg)/(2tan\alpha) = \mu_sN`

`(mg)/(2tan\alpha) = \mu_s (mg)`

`tan\alpha = (1)/(2\mu_s)`

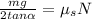
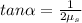
Therefore for equilibrium

`tan\alpha >(1)/(2\mu_s)`