Question

A proton orbits just at the surface of a charged sphere of radius 3.53 cm. If the speed of the proton is 2.02 X105 m/s, what is the charge on the sphere?

Answer 1

To solve this problem, apply the equilibrium condition given from the electrostatic force and the centripetal force of the body. Said equilibrium condition can be described under the function,

`F_c = F_q`

`(mv^2)/(r) = (kQ_(proton)Q_(Sphere))/(r^2)`

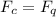
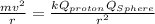
Here,

m = Mass of proton

Q = Charge of each object

k = Coulomb's constant

v = Velocity

Our values are given as,

`q= 1.6*10^(-19) C`

`m = 1.67*10^(-27) kg`

`v = 2.02* 10^5m/s`

`r = 3.53cm = 3.53*10^(-2) m`

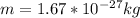
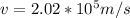
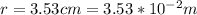
Rearranging and replacing we have,

`(mv^2)/(r) = (kQ_(proton)Q_(Sphere))/(r^2)`

`Q_(sphere)= (mv^2 r )/(kQ_(proton))`

`Q_(sphere) = ((1.67*10^(-27))(2.02*10^5)^2(3.53*10^(-2)))/((9*10^9)(1.6*10^(-19)))`

`Q_(Sphere) = 1.6704*10^(-9)C`

`Q_(Sphere) = 1.67nC`

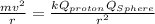
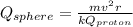
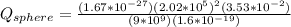
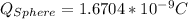
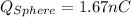
Therefore the charge on the Sphere is 1.67nC