Question

Verify that the function is a solution of the differential equation on some interval, for any choice of the arbitrary constants appearing in the function.

(a) y = c e^(2x) ; y' =2y

(b) y = (x^2)/3 + c/x ; xy' + y = x^2

(c) y = 1/2 + c e^((-x^2)/2) ; y' + 2xy = x

(d) y = (1+c e^((-x^2)/2)) ; y = (1-c e^((-x^2)/2) ; 2y' + x(y^2 -1) = 0

Answer 1

See details below

Explanation:

To verify that y=f(x) is a solution of the differential equation in some interval (where f is defined), we take derivatives respect to x using the usual rules (sum, product, chain rule, exponential,...)

a)
`y=ce^(2x)\rightarrow y'=(2x)'ce^(2x)=2ce^(2x)=2y`

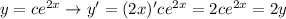
b)
`y=(x^2)/3+c/x \rightarrow xy'+y=x( 2x/3 -c/x^(2) )+(x^2)/3+c/x =3x^2/3-c/x+c/x=x^2`

c) The solution of the differential equation is slightly different (the function given is a solution only if c=0)

`y=1/2 + ce^((-x^2)) \rightarrow y'+2xy=((-x^2))'ce^((-x^2))+2x(1/2 + ce^((-x^2)) )=-2cxe^((-x^2))+x+2cxe^((-x^2))=x`

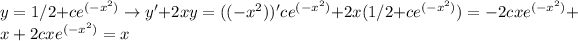
d)
`y=1+c e^((-x^2)/2))  \rightarrow 2y'+x(y^2-1)=2(-xce^(x^2/2))+x(1+2ce^(x^2/2)+c^2e^(-x^2)-1)=-2xce^(x^2/2)+2xce^(x^2/2)+c^2e^(-x^2)=c^2e^(-x^2)=0`

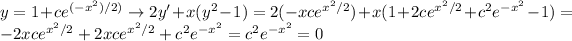
only if c=0, this also happens for the other function.