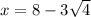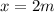Question

A particle is moving along a straight line such that when it is at the origin it has a velocity of 4 m/s. if it begins to decelerate at the rate of a= (-1.5v^1/2) m/s^2, where v is in m/s, determine the distance it travels before it stops.

Answer 1

To solve this problem we will apply the second law of kinematics that describes the position as a function of speed, time and its acceleration, as

`x = v_0t + (1)/(2) at^2`

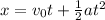
Here,

`v_0` = Initial velocity

t = Time

a = Acceleration

Our values are,

`t = 2`

`v_0 = 4m/s`

`a = -1.5√(v)`

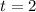
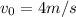
Replacing we have that

`x = v_0t + (1)/(2) at^2`

`x = 4(2)+(1)/(2)(-1.5√(v))(2)}^2`

`x = 8+2(-1.5√(v))`

`x = 8-3√(v)`

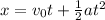
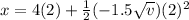
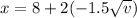
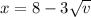
From this expression we could determine the position traveled, without considering that the given speed is the same assumed in the term of acceleration. Under this consideration we would have to v = 4m / s

`x = 8-3√(4)`

`x = 8-3*2`

`x = 2m`