Question

Shakina and Juliette set the car's initial velocity to zero and set the acceleration to +1.8 m/s^2, then clicked "start." Answer the following questions.

a. What is the car's displacement between 0 and 10.0 s?
b. What was the total distance traveled by the car during this time interval?

Answer 1

To solve this problem we will apply the linear motion kinematic equations for which we have that the distance traveled can be described in terms of the initial speed, time and acceleration. Our values are,

`u_0 = 0`

`a = 1.8m/s^2`

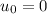
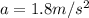
PART A) Applying the second kinematic law we have,

`s = u_0 t +(1)/(2) at^2`

Here

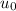`u_0` = Initial velocity

t = time

a = Acceleration

s = Position

Replacing,

`s = 0*10 +(1)/(2) 1.8*10^2`

`s = 90m`

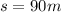
PART B) The distance traveled by the car in the range of 0 to 10 was linear. Therefore, said total displacement will be the same as previously found at point A. Therefore it will be 90m