Question

A small rock is thrown vertically upward with a speed of 22.0 m/s from the edge of the roof of a 30.0-m-tall building. The rock doesn’t hit the building on its way back down and lands on the street below. Ignore air resistance.

a. What is the speed of the rock just before it hits the street?
b. How much time elapses from when the rock is thrown until it hits the street?

Answer 1

To solve this problem we will apply the kinematic equations of linear movement. For this purpose we will begin to define the final speed of the body before hitting the street. The first equation will begin using the difference in velocities as a function of acceleration (gravity) and position. And the second will use the concept of acceleration, time and speed, to find the time variable.

PART A) Equation of motion is

`v^2-u^2 = 2as`

`v^2 = u^2+2as`

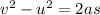
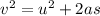
Replacing,

`v^2 = 22^2+2(9.8)(30)`

`v = 32.74m/s`

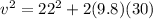
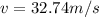
The speed of rock before hitting the ground is 32.74m/s

PART B) Equation of motion

`v-u=at`

`t = (v-u)/(a)`

`t = (32.74-(-22))/(9.8)`

`t = 5.58s`

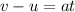
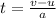
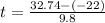
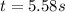
Therefore the time taken by the rock is 5.58s