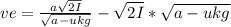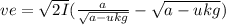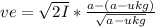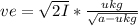Answer:
a)
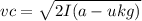
b)
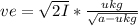
Step-by-step explanation:
Hi there!
a) Let´s find the work done on the block. Using the energy-work theorem we can find the speed of the block at the moment it hits the wall.
The energy-work theorem states that the change in the kinetic energy (ΔKE) of an object is equal to the work (W) done on that object:
W = ΔKE = final KE - initial KE
Since the initial KE is zero (the block is at rest), then:
W = final KE
To find the work done on the block, we have to find the resultant force (RF) acting on the block:
W = RF · I
I = lenght of the boxcar (distance traveled by the block).
The resultant force is calculated by adding all the forces acting in the horizontal direction (since the object is not accelerated in the vertical direction, the sum of vertical forces is equal to zero). Then:
RF = F - Fr
Where:
F = force applied by the car.
Fr = friction force.
The friction force is calculated as follows:
Fr = μ · N
Where:
μ = coefficient of kinetic friction.
N = normal force.
Since the only forces acting in the vertical direction are the normal force and the weight of the block, then N = Weight = m · g
Then, the friction force will be:
Fr = μk · m · g
Where "m" is the mass of the block
The resulting force will be:
RF = F - Fr
RF = m · a - μk · m · g
RF = m · (a - μk · g)
Then, the work done on the block will be:
W = RF · I
W = m · I · (a - μk · g)
Applying the work-energy theorem:
W = ΔKE = final KE
m · I · (a - μk · g) = 1/2 · m · v²
Solving for v:
2 · I · (a - μk · g) = v²
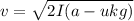
The speed of the block at the moment it hits relative to the car is
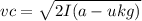
b) To calculate the speed of the block relative to the Earth, we have to find the speed of the car. Let´s use the equation of velocity of the block to find the time it takes the block to reach the wall:
v = v0 + ab · t (v0 = 0)
Where ab is the acceleration of the block
When the block reaches the wall, its velocity is
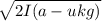 :
:
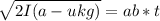
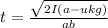
The velocity of the car is calculated as follows:
vcar = a · t
replacing
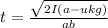
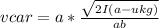
To find ab, let´s apply Newton´s second law:
RF = F - Fr = m · ab
m · (a - μk · g) = m · ab
ab = a - μk · g
Then, the speed of the car will be:
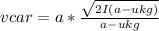
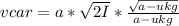
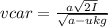
Then, the velocity of the block relative to the Earth will be:
velocity of the block relative to Earth = velocity of the car - velocity of the block relative to the car.
velocity of the block relative to Earth = ve = vcar - vc